Одинаковые треугольники разной площади
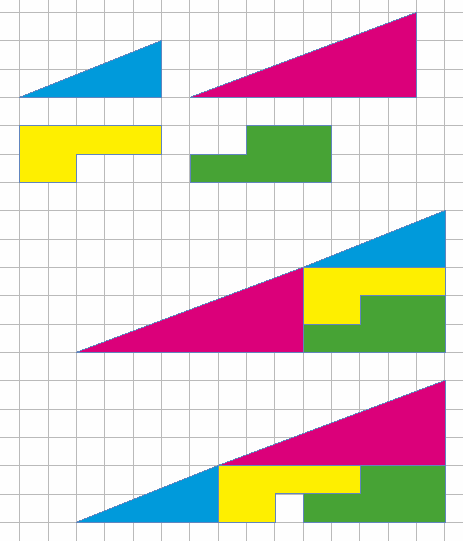
Бродя в выходные по Интернету, обнаружил такую головоломку — треугольник состоит из четырех элементов, но после их перестановки получившийся треугольник на первый взгляд точно такой же, но в нем появилась пустая клеточка.
http://xopoiiio.ru/main/ploshchad-dvukh-treugolnikov
Значит, площади их неравны?
Задача с ходу не решалась, но интрига затягивала — ведь раз компоненты обеих составных геометрических фигур одинаковые, то и площадь должна быть одинаковой — поэтому, не удовлетворившись обсуждением на сайте этого визуального обмана, повторил в индизайне эти элементы и сам сложил треугольники.
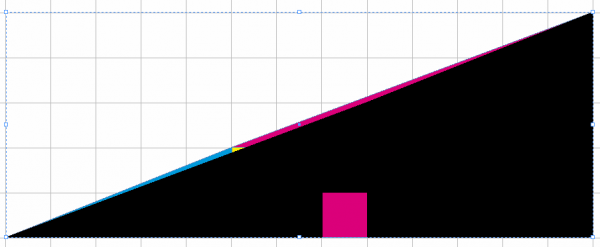
Файл лежит в архиве, и понять, где подвох, можно, присвоив обоим треугольникам режим прозрачности Difference и наложив их друг на друга.
Получается, что цветная полоска над гипотенузой черного треугольника равна по площади красному квадрату на нижнем катете.
Неожиданно, правда? : )
Если интересно, можете попробовать.
М.И.





 Скрипты Михаила Иванюшина
Скрипты Михаила Иванюшина InDesign ExtendScript API Adobe InDesign 2020 Object Model
InDesign ExtendScript API Adobe InDesign 2020 Object Model Indesign Snippets
Indesign Snippets
Получается, что конечный треугольник — не треугольник, по определению геометрии (http://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA).
Там обе геометрические фигуры не являются треугольниками. : )
При детальном рассмотрении первой фигуры можно увидеть излом на стыке красного и синего треугольников.
Что стало причиной публикации — мне показалось интересным, что, повторив Пером эти фигуры, присвоив режим прозрачности Difference и совместив их, без долгих объяснений становится очевидно, во что трансформировался квадратик. Люблю живые примеры, когда не нужно многословия, достаточно взглянуть на картинку. Посмотрите на сайте обсуждение этой задачки: как много слов, и они с трудом объясняют то, что становится сразу понятно, если воспользоваться хорошим инструментом.
Так что в ряде случаев индизайн годится и для подготовки учебных материалов по геометрии.
Не вёрсткой единой… : )
кстати у меня даже получилось, что площадь квадратика немного меньше площади той области над псевдогипотенузой..